Welcome to the OPTPDE Problem Collection

ccparfin1 details:

Keywords: analytic solution

Global classification: nonlinear-quadratic

Functional: convex quadratic

Geometry: easy, fixed

Design: coupled via volume data

Differential operator:

Design constraints:

State constraints:

Mixed constraints:

Submitted on 2013-05-27 by Fredi Tröltzsch. Published on 2013-06-21

ccparfin1 description:

Introduction

This example is an optimal control problem for a semilinear heat equation with cubic nonlinearity in a two dimensional domain. There are four time-dependent control functions restricted by box constraints. The example is constructed such that a locally optimal solution is explicitly known. It was used in the context of model reduction by POD to test an a posteriori error estimator for optimality, and appears in [Kammann et al., 2013, Section 4.2].

Variables & Notation

Unknowns

ui ∈ L2(0,T),i = 1,… ⁡,4 control functions y ∈ L2(0,T;H1(Ω)) ∩ H1(0,T;H1(Ω)′) ∩ L∞(Q)state variable

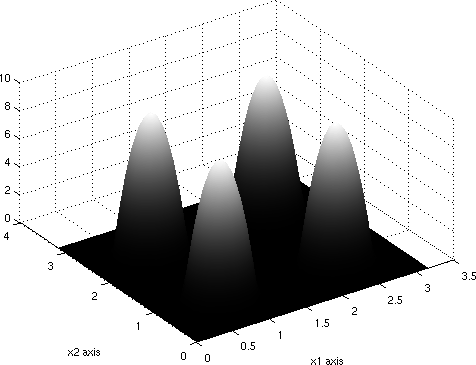
Given Data

Ω = (0,π)2 spatial domain Q = Ω × (0,T) computational domain T = 1 terminal time Σ = ∂Ω × (0,T) boundary ν outward unit normal on ∂Ω y0(x) = cos ⁡ (x1)cos ⁡ (x2), initial function yQ(x,t) = cos ⁡ (x1)cos ⁡ (x2)1 + 0.02(t − t2) − 0.03t2 cos ⁡ 2(x 1)cos ⁡ 2(x 2) desired state ay(x) = 0.01cos ⁡ (x1)cos ⁡ (x2) weight of terminal state w1(x) = max ⁡ 0,10 − 50(x1 − π 4 )2 − 50(x2 − π 4 )2) control weight1 w2(x) = max ⁡ 0,10 − 50(x1 − 3 4π)2 − 50(x2 − π 4 )2 control weight1 w3(x) = max ⁡ 0,10 − 50(x1 − 3 4π)2 − 50(x2 − 3 4π)2 control weight1 w4(x) = max ⁡ 0,10 − 50(x1 − π 4 )2 − 50(x2 − 3 4π)2 control weight1 βi(t) = proj ⁡ [−1,1] −t2 ∫ Ωwi(x)cos ⁡ (x1)cos ⁡ (x2)dx coefficient, i = 1,… ⁡,4 d(x,t) = ∑ i=14w i(x)βi(t) − 2cos ⁡ (x 1)cos ⁡ (x2) − cos ⁡ 3(x 1)cos ⁡ 3(x 2) distributed source term

The graphs of the functions w1,… ⁡,w4 are shown in Figure 0.1.

PIC

Figure 0.1: Weight functions w1,… ⁡,w4 for the controls ui.

Problem Description

Minimize 1 2∫ Q(y − yQ)2dxdt + ∫ Ωay(x)y(x,T)dx + 1 200∑ i=14 ∫ 0T u i(t)2dt s.t. ∂y ∂t (x,t) −△y(x,t) + y3(x,t) + d(x,t) = ∑ i=14w i(x)ui(t)in Q ∂y ∂ν(x,t) = 0 on Σ y(x,0) = y0(x) in Ω and |ui(t)|≤ 1in (0,T),i = 1,… ⁡,4.

Optimality System

The following optimality system for the state y, the control u, and the adjoint state p, given in the strong form, represents first-order necessary optimality conditions.

∂y ∂t (x,t) −△y(x,t) + y3(x,t) + d(x,t) = ∑ i=14w i(x)ui(t)in Q ∂y ∂ν(x,t) = 0 on Σ y(x,0) = y0(x) in Ω −∂p ∂t (x,t) −△p(x,t) + 3y2(x,t)p(x,t) = y(x,t) − y Q(x,t) in Q ∂p ∂ν(x,t) = 0 on Σ p(x,T) = ay(x) in Ω ui(t) = proj ⁡ [−1,1] −100∫ Ωwi(x)p(x,t)dx,i = 1,… ⁡,4 in (0,T).

Supplementary Material

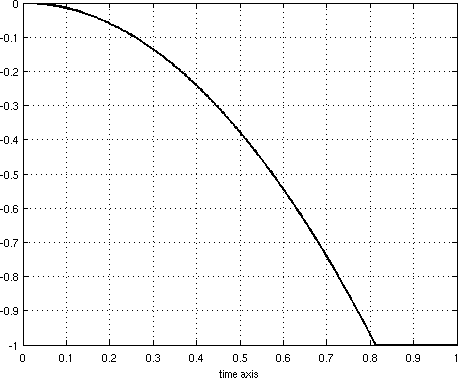
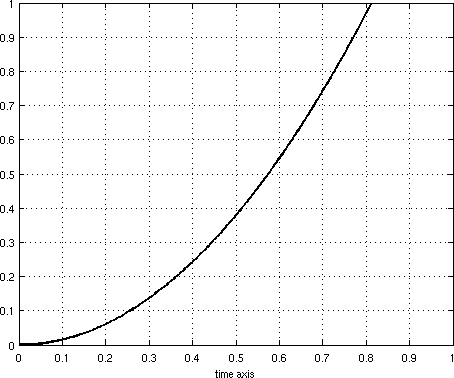
A set of locally optimal controls ui with associated state y and adjoint state p are known analytically.

ȳ(x,t) = cos ⁡ (x1)cos ⁡ (x2) in Q p̄(x,t) = t2 100cos ⁡ (x1)cos ⁡ (x2) in Q ūi(t) = proj ⁡ [−1,1] −t2 ∫ Ωwi(x)cos ⁡ (x1)cos ⁡ (x2)dx,i = 1,… ⁡ ,4in (0,T).

The controls are shown in Figure 0.2.

To show the local optimality of this solution, we verify that (ȳ,ū1,… ⁡,ū4) obeys the standard second-order sufficient optimality conditions.1 1 This analysis is not presented in Kammann et al. [2013] but it was carried out by the authors in 2014 (unpublished). To this end, we introduce the Lagrangian; writing u := (u1,… ⁡,u4), we define

ℒ(y,u,p) := J(y,u) −∫ Q ∂y ∂t −△y + y3 + d −∑ i=14w iui pdxdt.
The second-order derivative of ℒ with respect to (y,u) at (ȳ,ū,p̄) is
ℒ′′(ȳ,ū,p̄)(y,u)2 = ∫ Q y2 − 6ȳp̄y2 dxdt + 1 100∑ i=14 ∫ 0T u i(t)2dt ≥∫ Q0.94y2dxdt + 1 100∑ i=14 ∫ 0T u i(t)2dt ≥ 1 100∑ i=14 ∫ 0T u i(t)2dtfor all y ∈ W(0,T),u ∈ L2(0,T)4.

Notice that |ȳ(x,t)|≤ 1 and |p̄(x,t)|≤ 0.01 is satisfied. Invoking [Tröltzsch, 2010, Theorem 5.17], we obtain that ū is locally optimal with respect to the topology of L∞(0,T)4. (The quoted theorem is formulated for a control function u : Q → ℝ, but it obviously extends to the case u : Q → ℝ4.)

PICPIC

Figure 0.2: Optimal controls ū1,ū2. By symmetry, ū1 = ū3 and ū2 = ū4 holds.

Revision History

  • 2016–06–10: added comment on second-order sufficient conditions
  • 2014–10–30: formulas for the control weights w1,… ⁡,w4 corrected to match the calculations and figures in [Kammann et al., 2013, Section 4.2]
  • 2013–05–27: problem added to the collection

References

   E. Kammann, F. Tröltzsch, and S. Volkwein. A posteriori error estimation for semilinear parabolic optimal control problems with application to model reduction by POD. ESAIM. Mathematical Modelling and Numerical Analysis, 47(2):555–581, 2013. ISSN 0764-583X. doi: 10.1051/m2an/2012037.

   F. Tröltzsch. Optimal Control of Partial Differential Equations, volume 112 of Graduate Studies in Mathematics. American Mathematical Society, Providence, 2010.