Welcome to the OPTPDE Problem Collection

rddist2 details:

Keywords:

Global classification: nonlinear-quadratic

Functional: convex quadratic

Geometry: easy, fixed

Design: coupled via volume data

Differential operator:

Design constraints:

State constraints:

Mixed constraints:

Submitted on 2013-05-24 by Fredi Tröltzsch. Published on 2013-05-21

rddist2 description:

Introduction

This is a distributed optimal control problem for a semilinear 1D parabolic reaction-diffusion equation, where traveling wave fronts occur. The state equation is known as Schlögl model in physics and as Nagumo equation in neurobiology. In this context, various goals of optimization are of interest, for instance the stopping, acceleration, or extinction of a traveling wave. Here, we discuss the problem of re-directing a wave front after a certain time. The control is acting only on two subdomains near the boundary, which occupy the portion q of the entire spatial domain. This problem appears in [Buchholz et al., 2013, Section 5.2]. In the same paper, additional examples can be found which cover the other optimization goals mentioned above.

Variables & Notation

Unknowns

f ∈ L2(Q) control variable (forcing) u ∈ L2(0,T;H1(Ω)) ∩ H1(0,T;H1(Ω)′) ∩ L∞(Q)state variable

Given Data

Ω = (0,L) spatial domain L = 20 side length of domain Q = Ω × (0,T) computational domain Qq = (0,δ) ∪ (L − δ,L) × (0,T) control domain q = 2δ∕L = 0.6 portion of control domain T = 5 terminal time u0(x) = 1.23,x ∈ [9,11] 0,  elsewhere,  initial condition λ = 10−6 Tikhonov regularization parameter c = 450∕281 speed of the uncontrolled wave front uQ(x,t) = unat(x,t), t ∈ [0,2.5] unat(x + ct,2.5),t ∈ (2.5,T] desired state unat solution of the PDE (0.1) for f ≡ 0.

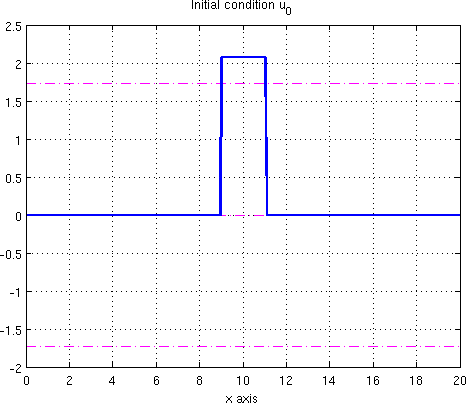
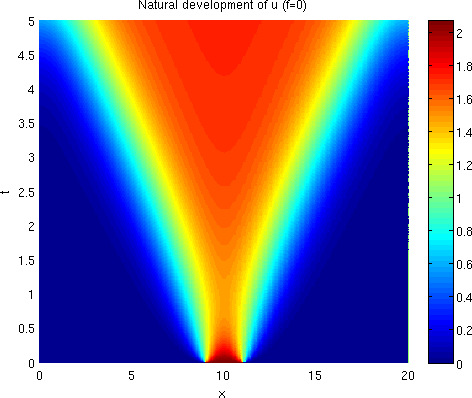
The natural uncontrolled state unat is shown in Figure 0.1. In the figure, the horizontal axis shows the spatial variable x while the vertical one displays the time t. The speed c of the uncontrolled wave front was determined numerically.

PICPIC

Figure 0.1: Initial state u0 (left) and natural uncontrolled state unat (right).

Problem Description

Minimize 1 2∬Q(u(x,t) − uQ(x,t))2dxdt + λ 2∬Qf2(x,t)dxdt s.t. ∂u ∂t (x,t) −∂2u ∂x2(x,t) + 1 3u3(x,t) − u(x,t) = f(x,t)in Q u(x,0) = u0(x) in Ω ∂u ∂x(0,t) = ∂u ∂x(L,t) = 0 in (0,T) (0.1) and f(x,t) = 0in Q ∖ Qq. Notice that the PDE has a non-monotone nonlinearity. The associated homogeneous elliptic (stationary) equation admits three different solutions; namely, the functions u1(x) ≡−3, u2(x) ≡ 0, and u3(x) ≡3.

Optimality System

The following optimality system for the state u, the control f, and the adjoint state p, given in the strong form, represents first-order necessary optimality conditions.

∂u ∂t (x,t) −∂2u ∂x2(x,t) + 1 3u3(x,t) − u(x,t) = f(x,t) in Q u(x,0) = u0(x) in Ω ∂u ∂x(0,t) = ∂u ∂x(L,t) = 0 in (0,T), −∂p ∂t (x,t) −∂2p ∂x2(x,t) + u2(x,t)p(x,t) − p(x,t) = u(x,t) − u Q(x,t)in Q p(x,T) = 0 in Ω ∂p ∂x(0,t) = ∂p ∂x(L,t) = 0 in (0,T), f(x,t) = −1 λp(x,t) in Qq f(x,t) = 0 in Q ∖ Qq.

Supplementary Material

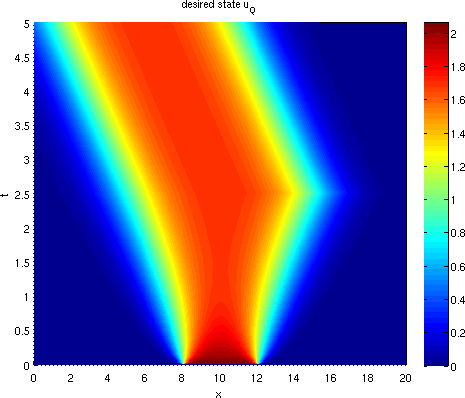
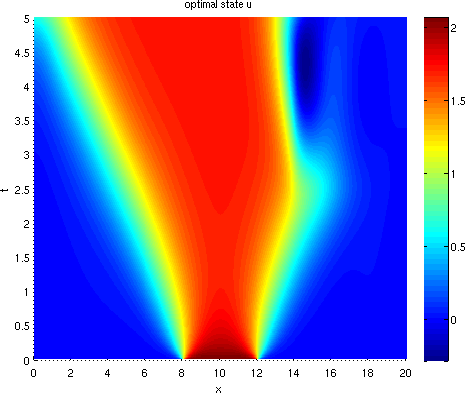
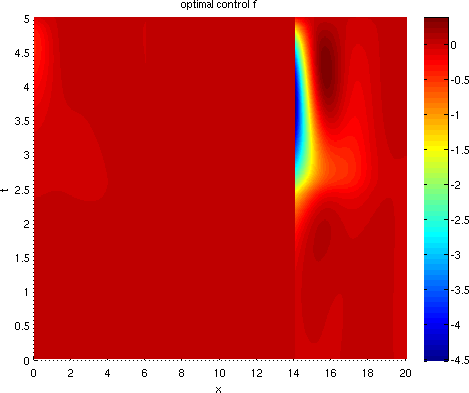
Figure 0.2 displays the desired state, as well as the optimal state and optimal control.

PICPIC
PIC

Figure 0.2: Re-directing a wave front with control support of size q = 0.6; desired state uQ (top left), optimal state u (top right) and optimal control f (bottom).

References

   R. Buchholz, H. Engel, E. Kammann, and F. Tröltzsch. On the optimal control of the Schlögl model. Computational Optimization and Applications, 56(1):153–185, 2013. doi: 10.1007/s10589-013-9550-y.